最終更新日:2024/08/16

コレは何？/What is this?

C++で行列/ベクトルの計算を手軽に超絶簡単にするArcsMatクラス。 ヘッダをインクルードするだけで手軽に使用可能！
これで、C++でMATLABと同じように気軽に行列計算ができます。行列とベクトルとスカラー間の加減乗演算、冪乗、LU/QR/コレスキー/SVDなどの行列分解、線形方程式系、逆行列、複素行列、 constexprでの行列の定義、「コンパイル時」での行列演算、MATファイルへの書き出し…等々ができます。旧版のMatrixクラスから大幅に改良されました。現在のところC++17に対応、後々C++20に移行予定。

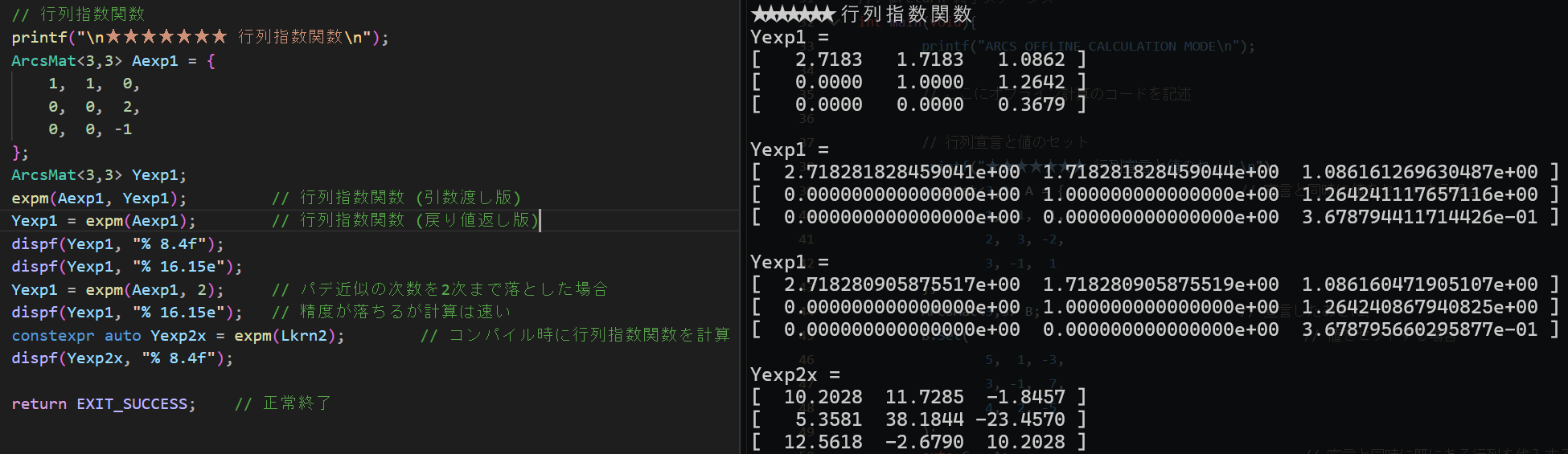
コンパイル時(≠実行時)に行列指数関数を計算する例

特徴/Feature

行列のサイズはコンパイル時定数
行列のサイズはコンパイル時に自動チェック
実行時ではなくコンパイル時に予め行列演算しておくことも可能
「コードの表記」が「数式の表記」に似てる
型はデフォルトでdouble型で省略可、適宜float、int、std::complex型などで宣言可能
計算結果を「引数で貰う場合」と「戻り値で貰う場合」の両方の関数を用意
内部のコメントが日本語
#include "ArcsMat.hh" するだけ、その他の依存関係はC++のstdだけ
メモリが縦方向に連続しているので縦ベクトル優先
要素番号(インデックス)は1から始まる

ダウンロード/Download

下記にアップロードしてあります。

テンプレートクラスなのでソースファイルの方はほぼカラです。 ARCS6には標準で搭載されています。上記はARCS6の内部に実装してあるものを抽出して出力してあります。

行列の定義の例/Example of Matrix Definition

行列の定義と初期化は、

ArcsMat<3,3> A = {
	1,  1,  1,
	2,  3, -2,
	3, -1,  1
};

のようにするとできます。 <3,3>がサイズで<縦,横>の順です。型はデフォルトでdouble型で、もしint型に変更するなら、

 ArcsMat<3,3, int>

とし、複素数型であれば、

 ArcsMat<3,3, std::complex<double>>

のようにします。その他、色々と方法があるので、サンプルコードを見てみてください。

行列演算子の一覧/List of Matrix Operators

使用可能な演算子の一覧は下記になります。

演算子	演算結果の意味
+	行列/ベクトル/スカラー間の加算
-	行列/ベクトル/スカラー間の減算
*	行列/ベクトル/スカラー間の乗算
/	「行列/ベクトル」と「スカラー」との間の除算
+=	行列/ベクトル/スカラー間の加算代入
-=	行列/ベクトル/スカラー間の減算代入
*=	行列/ベクトル/スカラー間の乗算代入
^	行列/ベクトルのべき乗
&	行列/ベクトルのアダマール積（要素ごとの掛け算）
%	行列/ベクトルの要素ごとの除算
v[ ]	縦ベクトルvの要素アクセス（普通の配列と同じ使い方）
A( , )	行列Aの要素アクセス（MATLABと同じ）
~A	行列Aの転置（複素行列の場合は自動的に共役転置）

行列に対して演算子が普通に使えます。行列AとBの掛け算であれば、

 C = A*B;

とするとできます。要素ごとの掛け算であれば、

 C = A & B;

とするとできます。さらにArcsMatでは、行列Aの転置(共役転置)は、

 C = ~A;

のように書けます。（どこかの他のライブラリで良くある A.transpose() などと書く必要ナシ！）また、演算子間の行列のサイズはコンパイル時に自動でチェックされ、もしそのサイズが不正であれば static_assert で引っ掛かって知らせてくれます。

行列要素へのアクセス/Matrix Elements

注意事項として、ArcsMatの要素番号はゼロ始まりではなく「1」から始まります（MATLABと同じ）。そして、要素へのアクセスの一例を挙げておくと、

 v[3] = 2.71;

とすると、縦ベクトルvの上から3番目に2.71を書き込みます。一方で、

 printf("% g\n", v[3]);

とするとvの3番目の要素を読み込んで表示します。また、

 A(2,3) = 3.14;

とするとAの上から2番目、左から3番目の位置に3.14を書き込みます。

 printf("% g\n", A(2,3));

のようにすると、Aの2行3列目の値を表示します。順番は (縦,横) でこれもMATLABと同一です。

主要な行列関数の一覧/List of frequently-used Matrix Functions

行列演算で良く使われる代表的な関数として下記のものが使用可能です。

関数	演算結果の意味
trace(A)	行列Aのトレース
diag(v)	縦ベクトルvの要素を対角に持つ行列を生成
getdiag(A)	行列Aの対角要素を縦ベクトルvとして抽出
det(A)	行列Aの行列式
inv(A)	行列Aの逆行列
rank(A)	行列Aのランク
eig(A) / eigvec(A)	行列Aの固有値と固有ベクトル
LU(A) / LUP(A)	行列AのLU分解
QR(A)	行列AのQR分解
LDL(A) / Cholesky(A)	行列AのLDL分解と修正コレスキー分解
SVD(A)	行列Aの特異値分解
Kron(A, B)	クロネッカー積
cross(A, B)	クロス積
vec(A) / vecinv(A)	vec作用素とその逆
expm(A)	行列指数関数
linsolve(A, B)	線形方程式 AX = B の解
...	等々

上記はほんの一部で、その他にも色々な関数を準備してあります。

行列関数の使用例/Usage of Matrix Functions

ほとんどすべての関数において、その使い方には大きく分けて２通り用意されています。
一例として、行列Aのすべての固有値を要素に持つ縦ベクトルvを得るには、

 eig(A, v);

のようにします。これは引数で結果を貰う場合です。旧来のC言語での流儀ですね。一方で、

 v = eig(A);

のようにして結果を得ることもできます。 ArcsMatではほとんどの関数で、上記の双方ともどちらの書き方でもオーケーです。読みやすさは後者に軍配が上がりますがコピーが生じ、前者ではコピーが発生しないので高速になる可能性があります。（ただし、最適化次第で同等になる可能性もある。キーワード：RVO/RVNO）

では、結果が２つ以上の複数の行列のときはどうするのか？例えば、固有ベクトルVと固有値の対角行列Dを得るには、

 eigvec(A, V, D);

として引数で渡して貰うか、

 std::tie(V, D) = eigvec(A);

のようにタプル(std::tuple)で貰うこともできます。上記はVとDが定義済みのときですが、定義と同時にするなら、

 auto [V, D] = eigvec(A);

のようにして得ることもできます（キーワード：構造化束縛）。 autoを使うと行列のサイズをコンパイラが自動で推論して定義してくれるので便利です。
ということで、ArcsMatでは上記のようにMATLABっぽい書き方もできます。

行列関数のコンパイル時計算/Compile-time Calculations

実行時ではなく、コンパイルの最中に行列の計算をすることもできます。
例えば、コンパイル時に行列Aの値が決定済みで、実行する前にそのAの行列指数関数を予め計算しておきたければ、

 constexpr auto Y = expm(A);

のように constexpr を付ければできます。ただし、行列Aも constexpr である必要があります。コンパイル時に事前に計算しておけば、実行時の計算時間が短くできます。 ArcsMatではほとんどすべての関数が constexpr に対応しています。ただし、画面表示系の関数に加えて、複素数(std::complex)を型に指定したときは constexpr非対応です(C++20移行時に対応予定)。

出力される行列が複数個の場合では、

 constexpr auto USV = SVD(A);
 constexpr auto U = std::get<0>(USV);
 constexpr auto S = std::get<1>(USV);
 constexpr auto V = std::get<2>(USV);

のようにします。上記は特異値分解で行列U、Σ、Vをコンパイル時に計算して、それぞれ std::get で取り出して格納する例です。この場合、実行時には既に特異値分解が終わっているので、SVDに掛かる計算コストはゼロです！

すべての関数一覧/List of Functions

公開メンバ関数等々の一覧のdoxygenドキュメントを下記に置いておきます。

ARCS::ArcsMat 公開メンバ関数

その他の行列演算の書き方の例

C++で行列演算をする際にどのように書けば良いかの一例を示しておきます。下記のコードを参照してみて下さい。

MATLABとの相違

下記の場合、ArcsMatの計算結果はMATLABの結果とは異なる場合があります：

行列分解の符号関係
複素数のときの行列分解
劣決定系のときの線形方程式の解

ただし、もちろん行列分解の結果としては正しいものです。分解した行列を乗算すれば元の行列に戻ります。（今後、なるべくMATLABと同一の数値が得られるように改修予定）

なぜ独自に開発するのか？

他にも線形代数ライブラリあるじゃん、なんでこんなんを独自に作ってるの？
→ 他の行列計算ライブラリのコード表記法の不満、見難ささ、導入の面倒くささ
→ ARCS6への標準搭載と付随する権利関係をクリアにしたい、constexprへの対応・コンパイル時計算＆チェックをしたい、コア部分を弄り回したい
→＋趣味。車輪の再開発で内製化することで、自身の従来の不満を解消。

要望受付中！

「こんな機能・関数があったら便利だなあ」というのがあったら横倉までご連絡下さい。暇を見つけて対応します。

ライセンス/License

このライブラリはMITライセンスです。商用でもご自由にお使いください。（ご一報頂けると喜びます）

MIT License
Copyright (c) 2011-2024 Yokokura, Yuki

Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.